「プロになるJava」ボツ原稿、今回は「13章 処理の難しさの段階」に入れようと思っていた、「アルゴリズムと計算量」の話です。
こういう話題でよくでる「こんな難しいプログラム組まないのでは?」という疑問についても最後にまとめています。
アルゴリズムと計算量
ここまでいろいろな処理の計算手順について紹介しました。こういった計算手順のことを アルゴリズム といいます。
同じ処理をするアルゴリズムはいろいろ考えられます。そのとき気になるのは実行性能の問題です。
ただ、実行性能はコンピュータによってクセがあるので、アルゴリズムそのものについてを考えるときにはそういったクセを取り除いて考えたいものです。
そこで、アルゴリズムの性能について考えるときには、データが増えるごとに計算時間や使用メモリがどのように増えていくかということを考えます。
この増え方のことを 計算量 といいます。計算時間に関する計算量を 時間計算量 、使用メモリに関する計算量を 空間計算量 といいますが、単に計算量と言ったときには時間計算量のことを表します。
リストの探索
アルゴリズムによる計算量の違いについて見てみましょう。 例えば次のように数値が昇順に並べられたListがあるとします。昇っていく順なので小さい数字が前にくる順番です。
var data = List.of(9, 15, 21, 24, 37, 47, 52, 78, 83, 87);
この配列に16や78といった数値が含まれているかどうか判定するプログラムを作ることを考えます。
線型探索
まず考えられるのが、Listの要素を先頭から順に値を確認して、求める値がListに含まれるかどうか確認する方法です。
src/main/java/projava/SearchSample.java
package projava; import java.util.List; public class SearchSample { static boolean search(List<Integer> data, int target) { for (int n : data) { if (n == target) { return true; } } return false; } public static void main(String[] args) { var data = List.of(9, 15, 21, 24, 37, 47, 52, 78, 83, 87); System.out.println(search(data, 16)); System.out.println(search(data, 78)); } }
16を探すとList中にないのでfalseになり、78を探すとList中にあるのでtrueが表示されます。
false true
拡張for文でデータを先頭から処理をして、該当する値があればtrueを返し、値がみつからないままループが終わった時にはfalseを返しています。
for (int n : data) {
if (n == target) {
return true;
}
}
return false;
このように頭から順にひとつずつデータを確認するような探索方法を 線形探索 といいます。
データが昇順に並んでることを利用すると、前から順に探していってデータが求める値より大きければ、それ以降には求めるデータがないことがわかります。
そこで次のように、途中で探索を打ち切ることで少し計算が速くなります。
src/main/java/projava/SearchSample.java
static boolean search(List<Integer> data, int target) { for (int n : data) { if (n == target) { return true; } else if (n > target) { return false; } } return false; }
また、この処理はStreamで書くことができます。Streamで書くと次のようになります。
src/main/java/projava/SearchSample.java
static boolean search(List<Integer> data, int target) { return data.stream() .anyMatch(n -> (n == target)); }
二分探索
データが昇順に並んでいるので、もっと効率のよい探し方があります。
先ほど、求める値よりデータが大きければそれより後に該当する値は存在しないことを使って、処理を少し速くしました。
同じように、求める値よりデータが小さければそれより前に該当する値は存在しないとも言えます。
そうすると、真ん中の値を取り出してどちら側にデータがあるかを見ていくことができます。
データが半分になったら、そのデータに対して同様に処理を行っていくと、最終的にデータがあるかどうかの判定ができます。
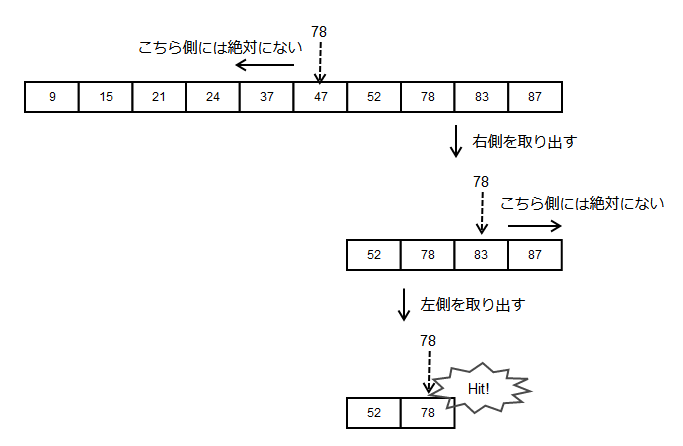
このような探索方法を 2分探索(にぶんたんさく) といいます。
2分探索は次のようなコードになります。
src/main/java/projava/SearchSample.java
static boolean search(List<Integer> data, int target) { if (data.isEmpty()) { return false; } else if (data.size() == 1) { return data.get(0) == target; } int midIndex = data.size() / 2; int midData = data.get(midIndex); if (midData == target) { return true; } else if (target < midData) { return search(data.subList(0, midIndex), target); } else { return search(data.subList(midIndex + 1, data.size()), target); } }
Listに対する再帰の処理では、データがないときや1件のときの処理を先に済ませておくのがコツです。
if (data.isEmpty()) {
return false;
} else if (data.size() == 1) {
return data.get(0) == target;
}
ここではListが空であればfalse、要素が1件であればその要素が求める値に一致するかどうかを返します。
真ん中の位置を計算して、その要素を得ます。
int midIndex = data.size() / 2; int midData = data.get(midIndex);
真ん中の要素が求める値であればtrueを返して処理を終わります。
if (midData == target) {
return true;
真ん中の要素が求める値よりも大きければ、求める値は前半部分にあるはずなので、subListメソッドで前半部分を切り出してsearchメソッドを再び呼び出します。
} else if (target < midData) {
return search(data.subList(0, midIndex), target);
残ったのは真ん中の要素が求める値よりも小さい場合なので、求める値は後半部分にあるはずなので、subListメソッドで後半部分を切り出してsearchメソッドを再び呼び出します。
} else {
return search(data.subList(midIndex + 1, data.size()), target);
こうして求める値がListに含まれているかどうかを判定できます。
練習
1. このサンプルではコードが単純化できるようにListを使っていますが、実際には整数については配列で扱うほうが効率がよいです。配列にして作り直してみましょう。
配列の分割を行う適切なメソッドはないので、Arrays.copyOfRangeメソッドを使って配列の部分コピーを作成することで同様の処理ができます。
2. 配列のコピーを行うのは効率が悪いので、コピーを行わずに処理できるようにしてみましょう
3. 前節の再帰を使ったループで24000を超えるとStackOverFlowErrorが発生していました。エラーが発生する回数を正確にみつけるときにも2分探索の考え方が使えます。実際に2分探索の考え方を使ってエラーが発生する回数をみつけてみましょう。
計算量
それではリストの探索の計算量を考えてみましょう。
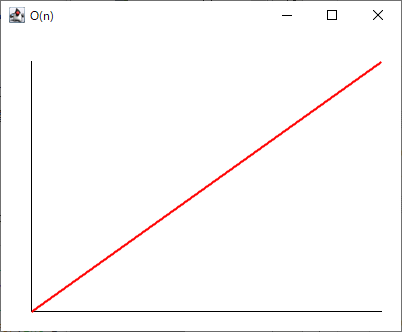
線形探索では、データが増えれば増えた分だけ処理量が増えます。データが100倍になれば100倍、1000倍になれば1000倍の処理量がかかります。
データ量と処理量の関係は次のようになります。
線形探索で探索を途中で打ち切るようにする改良を紹介しましたが、この場合は処理量は平均すると半分くらいになるものの、データ量が増えたときの処理量の増え方は変わりません。
線形探索ではデータが増えれば増えただけ処理量が増えます。このとき、前処理にかかる時間をA、1回の処理時間をB、結果出力にかかる時間をCとして、データ量をnであらわすと、処理時間tはt = A + Bn + Cで表せます。
ただ、ここでデータ数が大きくなったときには前処理の時間Aや結果出力の時間Cはどんどん無視できるようになります。また、1回の処理時間Bは実装方法でも変わり、ここではデータ数によって処理時間がどのように増えるかを知りたいので、処理時間Bも無視できます。
このように、式を単純化して計算時間を見積もる方法を 漸近的解析といいます。漸近的解析で求められた大ざっぱな計算時間は 漸近的記法 で表します。線形探索の計算時間を漸近的記法で表すとt=O(n)となります。計算時間を大文字のOを使って表す記法を big-O記法 といいます。
アルゴリズムの計算量を表すときは、big-O記法を使って「線形探索の計算量はO(n)だ」のようにいいます。
2分探索では、データが2倍になったときに処理が1回増えるので、データが1000倍になっても処理は10回増えるだけです。データが増えてもデータが増えたほどに処理量は増えません。
2分探索でのデータ量と処理量の関係は次のようになります。

2分探索の計算量はO(log n)になります。logなんてよくわからない、という人も多いと思いますが、処理が進むごとにデータ件数が一定の比率で減っていく場合に計算量がO(log n)になると覚えておけばいいと思います。2分探索では処理が進むごとにデータ件数が1/2に減っていきます。
このように、同じ処理でもやりかたによってデータが増えたときに遅くなる度合いが変わります。
移動平均の処理では、データ件数をn、ウィンドウサイズをwとすると、最初の処理の場合の計算量はO(n × w)、効率化した場合の計算量はウィンドウサイズに関わらなくなるのでO(n)となります。
よく見かける計算量には次のようなものがあります。
| 計算量 | 処理の傾向 | 実際の処理例 |
|---|---|---|
| ループがない | 配列から指定要素を得る | |
| 処理が進むごとに処理件数が一定割合で減る | 2分探索 | |
| 処理が進むごとの処理件数が一定件数減る。データ件数分のループ | 線形探索 | |
| 処理が進むごとに一定割合で減ったデータに対して件数分のループ | 昇順並べ替え | |
| データ件数分の二重ループ | 平面上の点から、一番距離が近い組み合わせを得る | |
| 複数の要素のすべての組み合わせを得る | 容量の決まったナップサックに重さの違う複数の品物をギリギリまで詰める組み合わせを得る | |
| 複数の要素のすべての順列組み合わせを得る | セールスマンが複数の会社に営業に行くときどの順番が最も移動距離が短いか判定する |
処理したいデータ量が多くなるときは、データ量に対してどのように処理量が増えていくか、計算量を考えることが大切になります。
特に、計算量がや
になると少しデータが増えただけで計算が終わらなくなってしまいます。手元で少ないデータで動かすときには大丈夫なのに、実際の運用を始めてデータが増えると重くて使い物にならないということにもなりかねません。
データ量に対する計算時間の伸びについて意識できるようになりましょう。
こんな難しいプログラム組まないのでは?
実際には昇順に並んだ配列から要素を探すにはArrays.binarySearchメソッドがあります。難しい処理はライブラリやフレームワークが提供さていることが多く、自分で実装する必要性は高くありません。
それではこのような難しいことは勉強する必要がないのでしょうか?
一部に難しい処理が現れることがある
アプリケーションを作るとき、おそらくプログラムのほとんどは簡単な処理として書くことができます。ただ、プログラムが大きくなってくると、その中での一部に難しい処理が現れてきます。
そういった、一部に現れる難しい処理を適切に書けることは、安定したアプリケーションを作るうえで大切になります。
それぞれの処理が簡単でも全体では難しい処理をすることがある
データ中から重複を省く処理を書くことはありませんが、Twitterのような投稿機能を実装するときに直前と同じ投稿を無視するような処理を書くことはあります。
ループの中で状態遷移するプログラムを書くことはありませんが、注文を行ったら「注文中」、運営者が商品発送を行ったら「配送中」、商品が届いたら「完了」のように状態が変わるシステムを組むことは多くあります。
システム内の状態が変わるのに日数がかかったりフレームワークに隠されたりして、それぞれの状態ごとの処理を別の場所に書くことも多いです。そうすると、個別の処理は簡単に見えます。
例えば状態遷移のプログラムのcase句を抜き出せば、条件によって値を変えるかメソッドを抜けるという簡単な処理になっています。
case FRAC_START, FRAC -> {
if (ch >= '0' && ch <= '9') {
state = FloatState.FRAC;
} else {
return false;
}
}
目の前の処理の簡単さにだまされて状態遷移に気づかず実装を進めたとき、いきあたりばったりなコードを書いてしまい、運用を始めると条件によって変な動きをすることがわかり、その場しのぎの修正をすると必要以上に複雑になる、ということもよく見かけます。
「こんな難しいプログラム組まないのでは?」という疑問の答えとしては、「個々の処理で難しいプログラムを書くことは少ないけど、プログラム全体としてこういった難しさがでてくることは多い」となります。
簡単に見える処理を積み上げていくといつのまにか難しい処理になっているのがプログラムです。
ほかの人が勉強していないので差別化できる
普通の入門書にはこういった難しい話は載っていません。つまり、ほとんどの入門者はこういったことを勉強しないのです。勉強しようと思ったときには難しめの本が必要になってギャップがおおきく、手を出しづらいということもあります。
プログラマはデキル人になるほど人数がすごく少なくなるという状況があります。
今後、単純なWebサイトや企業システムの構築はどんどん簡単になり、そのような簡単なサイトやシステムを組める人はどんどん増えていきます。その裏では難しい部分も増えていきますが、難しいプログラムが組める人はそこまでは増えないと思っています。
つまり、作るものや作る人について、難しいものと簡単なもの、難しいことができる人と簡単なことだけできる人が二極化していくことが予想されます。
そういった場合、ここに書いたことをしっかり理解できれば、プログラマ全体としてかなり上位に入ることができるようになります。
2023/2/8 追記 ブラウザのレンダリングでn<sup>2</sup>などがn2のように表示されていたのでtex記法に書き換え
