2次ベジェ曲線から3次ベジェ曲線への変換

点p1と点p2を通って、中間の制御点が点sになる2次のベジェ曲線を3次のベジェ曲線に変換するときの制御点v, wは、それぞれp1〜a,p2〜aの2/3の点になる。

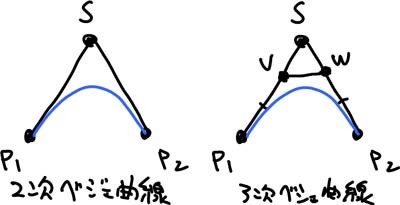
つまり、2次ベジェ曲線のオブジェクト

new QuadCurve2D.Double(
    p1x, p1y, 
    sx, sy, 
    p2x, p2y)

は、次の3次ベジェ曲線のオブジェクトと同じ形になる。

new CubicCurve2D.Double(
    p1x, p1y, 
    (p1x + 2 * sx) / 3, (p1y + 2 * sy) / 3, 
    (2 * sx + p2x) / 3, (2 * sy + p2y) / 3, 
    p2x, p2y)

これは、数式的に等価。
つまり、3次ベジェ曲線の式
$\large t^3 p_1 + 3 t^2 (1-t) v + 3 t (1 - t) ^2 w + (1-t)^3 p_2$
に、 $v=\frac{p_1 + 2 s}{3},w=\frac{2 s + p_2}{3}$ を代入すると
$\large t^2 p_1 + 2 t (1-t) s + (1-t)^2 p_2$
のような2次ベジェ曲線の式になる。

求め方。
3次ベジェ曲線 $\large t^3 p_1 + 3 t^2 (1-t) v + 3 t (1 - t) ^2 w + (1-t)^3 p_2$ と2次ベジェ曲線 $\large t^2 p_1 + 2 t (1-t) s + (1-t)^2 p_2$ が等しくなるv,wを求めればいいのだけど、求める値が２つあるので、ちゃんと値を求めるためには、もうひとつ式が必要。
ということで、傾きも同じになるはずなので微分したものも同じという条件も加える。
そうすると、次の連立方程式をv, wについて解けばいいことになる。
$\left.\begin{eqnarray}t^3 p_1 + 3 t^2 (1-t) v + 3 t (1 - t) ^2 w + (1-t)^3 p_2=t^2 p_1 + 2 t (1-t) s + (1-t)^2 p_2\\(t^3 p_1 + 3 t^2 (1-t) v + 3 t (1 - t) ^2 w + (1-t)^3 p_2)\frac{d}{dt}=(t^2 p_1 + 2 t (1-t) s + (1-t)^2 p_2)\frac{d}{dt}\end{eqnarray}\right\}$

で、まあ、こんな連立方程式を手計算で解くのは面倒なので、Maximaに解いてもらう。
http://phe.phyas.aichi-edu.ac.jp/~cyamauch/maxima/

a:t^3*p1 + 3*t^2*(1-t)*v + 3*t*(1-t)^2*w + (1-t)^3*p2;
b:t^2*p1 + 2*t*(1-t)*s + (1-t)^2*p2;
solve([a=b, diff(a, t)=diff(b, t)],[v, w]);

そうすると、こんな答えが出てくるって寸法。
$\large v=\frac{2 s + p_1}{3},w=\frac{2 s + p_2}{3}$
計算苦手でも、大丈夫。