ガウシアンカーネルのパラメータを自動的に求めてみる

サポートベクターマシンでよく使うガウシアンカーネルでは、パラメータが重要になるということを書きました。
で、ちょうどいいところに、id:audioswitch:20080730で、そのガウシアンカーネルのパラメータを自動的に求める方法が書かれていたので、試してみました。
σ^2=100程度の数値が出てきます。(リンク先でのパラメータはσとかいてますが、ぼくのところでは同じ値をσ^2としてます。)

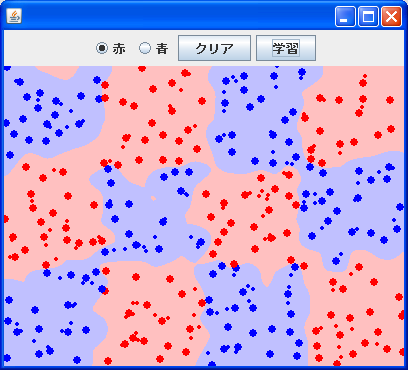
今回のデータでは、だいたいいい感じだけど、もう少し大きい数値のほうがいいかな〜という感じですね。それにしても、とりあえずの値を求めるにはよさそうです。
関係ある部分のソースだけを書いておきます。

private void btnLearnActionPerformed(java.awt.event.ActionEvent evt) {
    if(patterns.size() == 0) return;
    solveGaussianParam();
    learn();
    learned = true;
    paint();
    canvas.repaint();    
}

    void solveGaussianParam(){
        double s = 0;
        int count = 0;
        for(Map.Entry<Integer, Point> p1 : patterns){
            double m = Double.MAX_VALUE;
            for(Map.Entry<Integer, Point> p2 : patterns){
                double d = (p1.getValue().x - p2.getValue().x) * (p1.getValue().x - p2.getValue().x) +
                        (p1.getValue().y - p2.getValue().y) * (p1.getValue().y - p2.getValue().y);
                if(d == 0) continue;
                if(d < m) m = d;
            }
            if(m == Double.MAX_VALUE) continue;
            s += m;
            ++count;
        }
        sig = Math.sqrt(s / count);
        System.out.println(sig);
    }

    double sig = 35;

    double kernel(Point x1, Point x2){

        //ガウシアンカーネル
        double n = (x1.x - x2.x) * (x1.x - x2.x) + (x1.y - x2.y) * (x1.y - x2.y);
        return Math.exp(-n / (sig * sig));//5 1.2 .5は分散の2乗
    }